蒙提霍尔问题（三门问题、山羊汽车问题）

这个问题大致出自美国的电视游戏节目，问题的名字来自该节目的主持人蒙蒂·霍尔。参赛者会看见三扇关闭了的门，其中一扇的后面有一辆汽车或者是奖品，选中后面有车的那扇门就可以赢得该汽车或奖品，而另外两扇门后面则各藏有一只山羊。当参赛者选定了一扇门，但未去开启它的时候，知道门后情形的节目主持人会开启剩下两扇门的其中一扇，露出其中一只山羊。主持人其后会问参赛者要不要换另一扇仍然关上的门。问题是：换另一扇门会否增加参赛者赢得汽车的机率？

这里肯定是要忽略掉羊叫等干扰因素，一种看法是只剩了两个，换与不换都是二分之一概率，其实不然，正确的选择是换门，赢得汽车的机率是2/3。

可以从以下几个思路来看：
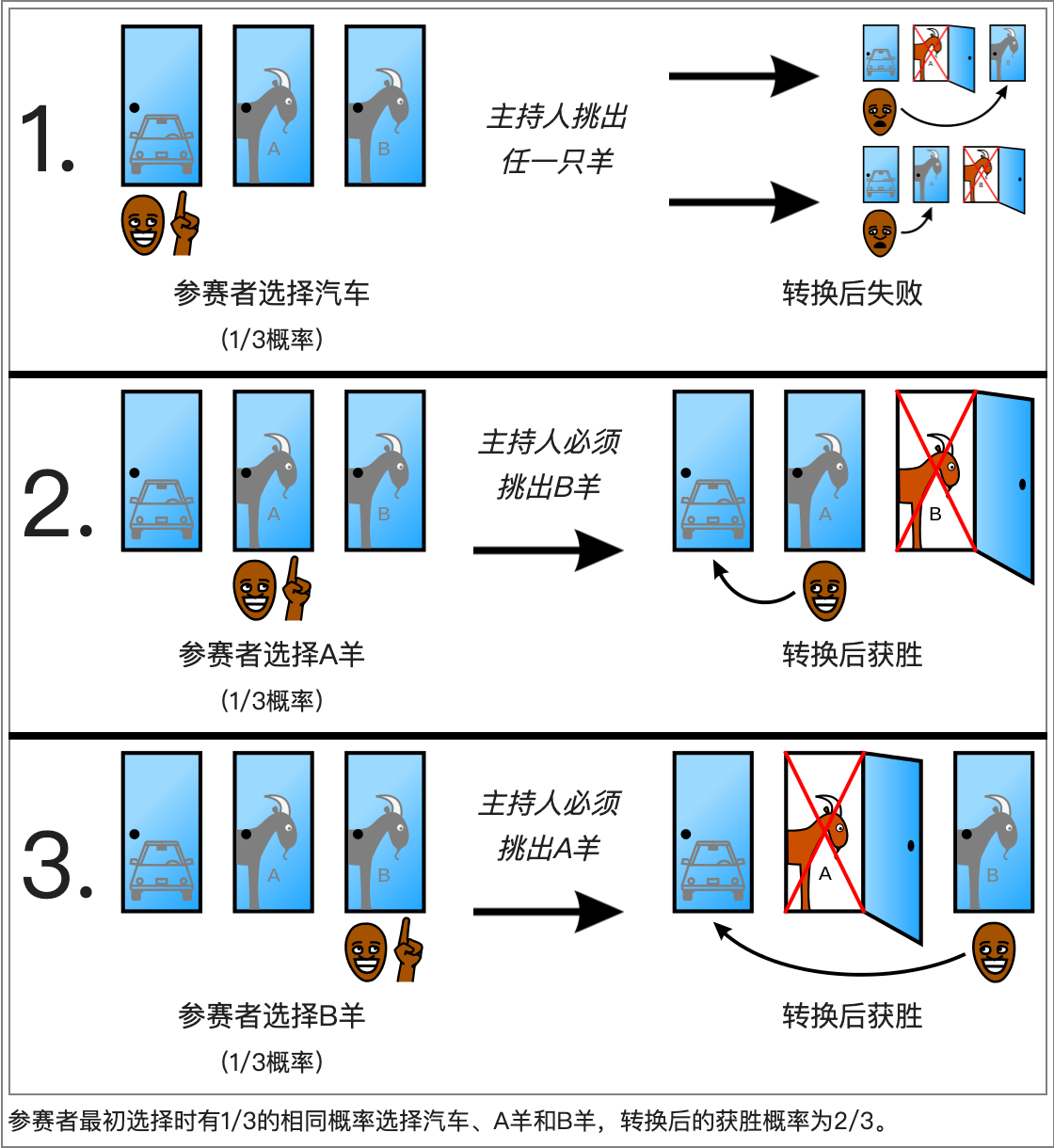
1.将未选中的看做一个整体，这部分是2/3的概率猜中奖品，选中的那一个是1/3概率。当去掉未选中之一时，未选中部分还剩一个，但整体概率从第一轮选择来看还是2/3，而自己在第一轮选择那个门猜中奖品的概率还是1/3。所以，换另一扇门，会将中奖概率提升到2/3.

2.来自中文维基百科

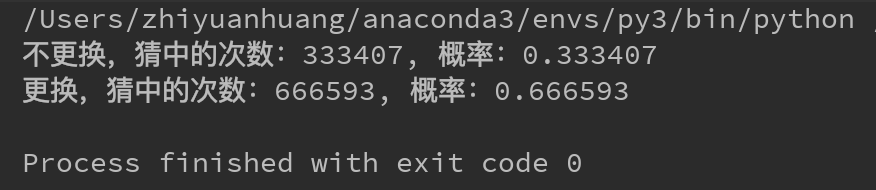
3.代码实现

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17


import random
times = 1000000  # 实验次数
x = 0  # 第一次选择后，不再更改，猜中的次数
y = 0  # 开门后，更换选择，猜中的次数
for sample in range(times):
    doors = [1, 0, 0]
    random.shuffle(doors)
    f_choice = random.choice(doors)
    if f_choice == 1:
        x += 1
    doors.pop(doors.index(f_choice))
    doors.remove(0)
    s_choice = doors[0]
    if s_choice == 1:
        y += 1
print("不更换，猜中的次数：%s, 概率：%s" % (x, x/times))
print("更换，猜中的次数：%s, 概率：%s" % (y, y/times))

Contents